Prof. Dr. Obádovics Gyula

Hogyan kellene használni az oktatásban az elektronikus eszközöket? Miért fontos a matematika tanulása?

Szeretettel köszöntök mindenkit, remélem, hogy így hallható lesz minden irányba. Nyolcvan éven keresztül én csak állva adtam elő. Sajnos a lábaim gyengék, ezért lehet, hogy öt vagy tíz perc múlva le fogok ülni, így nem a szokásos helyen tartom meg az előadást, hanem itt az elnökségi asztal mögött.

Nagyon komoly probléma az, amikor arról kell beszélni, hogy miként használjuk az elektronikus eszközöket a matematika tanítása szempontjából. Egy érdekességgel szolgálhatok itt mindjárt. Valamikor a matematikát, a műszaki egyetemet az első félévben ezzel a számítógéppel oldottuk meg, a logarléccel. A logarlécen megtalálhatók voltak a trigonometriai függvényértékek is, a logaritmusfüggvény-értékek is. Szorozni, osztani, kivonni, tudott. Az első fél év végén kötelező volt minden mérnökhallgatónak vizsgát tenni a logarléc-tudományból is. Miért volt ez nagyon lényeges? Minden mérnöki számításnál – és általában a matematikai feladatok megoldásánál – szerintem döntő az, hogy meg tudjuk becsülni azt, hogy körülbelül milyen érték várható. Ezt azért merem így mondani, mert a drága unokáim, mint egy orgonán, úgy játszanak a számítógépen, beütnek mindent, és azt mondják, ez az eredmény jó. Én viszont gyakran mondom nekik: valami baj van, mert ez ezerrel vagy több ezerrel eltér a várható értéktől. Hát miért? A számítógép jól dolgozik. – vágnak vissza nekem. Mondom: igen, igen, de mit ütöttél be? Meg tudnád becsülni, hogy milyen a várható értéke ennek a műveletnek? Fogalmuk sincs.

Nagyon sajnálatos szerintem az, hogy az általános iskolában és a középiskolában nem fordítanak nagyobb gondot arra, hogy az eredmény megbecsülésével is valamilyen módon tudjanak foglalkozni. Ez azért volt nagyon lényeges régen, mert amikor még tekerős masinával kellett számításokat végezni, és volt olyan házi feladat a hallgatóknál is, ami nyolcórás munkát jelentett. Fogalma sem volt, hogy mi várható eredményként. Nyolc órát dolgozott a tekerős számológéppel, hibás eredményt kapott. Kezdhette újra elölről a számítást.

Ma van számítógép, és van mesterséges intelligencia. Már a fejemhez vágja az unokám is, hogy mit vacakolsz ezzel a géppel? Hát kérd meg az MI-t megkapod az eredményt. Nem kell tovább dolgozni, mert általában délelőttönként még mindig matematikával foglalkozom, és a számítógép előtt ülök. Már várják, hogy befejezzem, gyerünk focizni jelszóval csábítgatnak ki, hagyd abba a munkát, mondják, majd ők megoldják. Már többet tud a számítógépről a 10–12 éves dédunokám, mint amennyit én valaha is tanultam. Úgyhogy nagyon érdekes tapasztalatokat lehet szerezni. Feltétlenül fontos lenne bebizonyítani nekik, hogy bizony nagyon fontos a becslési érték elérése.

Egy nagyon egyszerű példát szeretnék mondani. A kétismeretlenes, elsőfokú egyenletrendszer középiskolai grafikus megoldása könyvekben megtalálható. Már ismerik, hogy a kétismeretlenes egyenleteknél az első egyenletből egy egyenest lehet rajzolni az XY-koordinátarendszerben. A második egyenletből szintén egy egyenest lehet rajzolni. A két egyenes metszéspontját grafikusan, jó szerkesztésnél általában két-három jegy pontossággal – logarléc pontossággal – le lehet olvasni az ábráról.

Igen ám, de mi van akkor, hogyha az a két egyenes majdnem fedi egymást? Lehet, hogy valahol a plusz végtelen felé, vagy éppen a mínusz végtelen felé metszik egymást. Ha az egyenletrendszer együtthatói mérési eredmények, akkor a kerekítéssel egy-két százezred különbséggel is változhat az együttható. Az ilyen egyenletrendszer megoldása a plusz százezerből a gyökök értékénél mínusz százezret fog kihozni.

Előfordul már a középiskolában is, hogy az egyenlet megoldásának sokféle fajtája van, de a determinánsokat is ismerik. Abban a pillanatban, hogy kétszázezreddel – például egy mérőműszerről leolvasott és becsült értékeket – megváltoztatok, az egyetlenegy együttható megváltoztatása, a determináns értékét pozitívról negatívra változtathatja, azaz egyetlen pillanat alatt a plusz százezer értékű gyök mínusz százezer értékre változik.

A példa talán érzékelteti, hogy az elektronikus eszközöket annak megfelelően kell használjam, amint segítik a munkámat. Az ember-gép kapcsolat helyett, lassan ott tartunk, hogy gép-ember kapcsolat van, gépfüggők vagyunk. El kell érni, hogy a hallgatók megtanulják a gépek ésszerű használatát. Tanítsunk és ne oktassunk, mert ha én tanítok, akkor látom a szemekből, hogy érti vagy nem érti már a diák, amiről beszélek.

Nagyon lényeges, hogy a matematikát az órán megértsék és alkalmazni is tudják. Ha ez a kettő együtt van, akkor a tanítás elérte a célját. Például egy matematikai kongresszuson egy gyönyörű szép tételt mutatott be az egyik akadémikus, egy sor tétel, egy sor bizonyítás, hátralépett, gyönyörű. Erre egy mérnök-matematikus fölállt és azt mondta: nagyon tetszik a professzor úr előadása, szeretném alkalmazni az eredményét a saját munkámhoz. A válasz ez volt: az már izzadságszagú, én azzal nem foglalkozom. Tehát a matematika önmagában nem elég, hogy megismerjünk újabb és újabb módszereket, hanem a megvalósítás, az alkalmazás – különösen a műszaki területen – vezet oda, hogy a végeredmény megfogható legyen, máskülönben nem lehet hidat építeni, nem lehet útpályákat építeni. Tehát rá kell egyszer ébredni arra, hogy a gyönyörű szép, egész értékű megoldások – amik előfordulnak a középiskolai és általános iskolai példatárakban – becsaptak bennünket.

Nélkülözhetetlen, hogy olyan számítási eljárásokat is megismertessünk, amelyek a fokozatos közelítés, a szukcesszív approximációs módszerek témakörébe tartoznak, mert egy másik nagyobb problémát jelentő dolog szerepe felerősödött: a kerekítési hiba, a halmozódás kiemelt szerepet kell kapjon, hiszen a számítógép végtelen sokszor végzi a munkát, a részeredményeket újra felhasználja, de az már nem pontos, hanem kerekített érték.

Gondoljunk arra, hogy amikor nagyméretű lineáris rendszerek megoldásáról van szó, akkor bizony még a 16 jegy pontossággal dolgoztatott gép eredményét sem lehet az előírt hibakorláttal kiszámítani a kerekítési hibák halmozódása következtében. 1948/49-ben, az atombomba létrehozása, fejlesztésének a számítása idején mutatkozott meg először ez a probléma. Az alkalmazott numerikus módszereket meg kellett változtatni, mert a gép dolgozott, ezerszer ezres nagyságú számtáblázat alapján folyt a munka. A bomba területén öt kilométer, tíz kilométer, ötven kilométer körzetben felvett pontokhoz tartozóan írták fel az egyenletrendszereket, és az ezerszer ezres adat táblázatból kellett elvégeztetni a számítást. A kerekítési hiba halmozódása miatt használhatatlan eredményt kaptak. Neumann János volt az egyik abban az időben, aki a témával kellett, hogy foglalkozzon, és a kerekítési hiba halmozódására nem érzékeny számítási módszereket dolgozzon ki.

Tehát van számítógép ma már, mindent meg tud oldani, amit én kérek a számítógéptől, amit én valamilyen – feldolgozásra alkalmas – formában közöltem a számítógéppel. Nem a gép maga intelligens, tőlem függ az eredmény.

Nagyon sok lehetőség áll már rendelkezésre – sok millió ember vagy sok ezer számítógép közreműködésével –, hogy a feladataimat meg tudjam oldani. Ez már természetes a ma felnővő ifjúságnak olyan értelemben, ahogy természetes az autó, amibe beül és már tudja vezetni. A számítógép is fejlődik a fiatalokkal együtt, mind többet és többet tud nyújtani.

Ez már nagyon jó, de az a diák, aki egy számítógéppel együtt nőtt fel, észre sem veszi, hogy mi az a segítség, amit a matematika vagy a fizika megtanulása adott neki a feladatai megoldásához, mert a számítógép segítségével sokkal gyorsabban, jobban, egyszerűbben jut az eredményhez. Nem veszi észre, mert neki ez így természetes. De egy-két szemléltető példa segítségével rá kell vezetni őket, hogy a gép elkövethet hibát is, hogy aszerint használom a gépet, amennyiben segítséget tud nyújtani számomra az adott feladathoz, mert helyettem nem fog megoldani mindent a gép.

Egy másik ilyen érdekes témakör az, hogy olyan típusú egyenleteket is tudunk a gép segítségével vizsgálni, amelyekről nem tudjuk pontosan, hogy mit is jelentenek.

Például, ha valaki így tanítaná most a függvénytant, hogy azt mondja a gépnek:

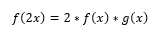
Ki tudja, hogy ez éppen mit jelentene függvényegyenletileg?

A számítógép nagyon szépen igyekezett megoldani a problémát, függetlenül attól, hogy nem adtam halmazt néki. Egyből elő tudta állítani azokat a lehetőségeket, amelyek valamilyen megoldást jelenthetnének. Tudjuk például, hogy

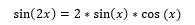
Ha a tanár így kezdi bevezetni a trigonometrikus függvényt, hogy

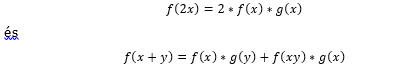
Mely függvények tesznek eleget a két egyenletnek?

Azt hiszem, ezt a tanárt kizavarnák az óráról, mert senki nem értené meg a trigonometria alapösszefüggéseit.

Még ma is nagyon gyakori, hogy egy egyetemi előadó belép a terembe és már mondja is: egy adott halmazban értelmeztem egy összeadást, egy szorzást, és ebben a halmazban … Mondja a szöveget, mondja a szöveget, de az a szegény egyetemi hallgató, aki először van jelen egy ilyen órán, inkább hazamenne.

Úgyhogy ezért hangsúlyoztam nem mindegy, hogy oktatunk vagy tanítunk. Én a tanítás mellett vagyok, az egyetemen is ezt csináltam, és ezért született egy olyan kis könyvecske, amelyik tartalmazza mindazokat a kérdésköröket, amelyeket a hallgatók kérdései alapján problémásnak láttam – nem is beszélve a klasszikus, igen nehézkes tételmegfogalmazásokról, amelyeket bizony sok-sok éjszakán keresztül magyarról magyarra fordítottam, hogy érthető legyen a tétel is, de érthető legyen az a lépéssor is, amit ott szövegesen leírtak. Máskülönben azok a hallgatók, akik nem megfelelő előképzéssel jöttek az egyetemre, azok elvesztették volna a fonalat már az első perctől kezdve. Az ötvenes évek elején még az volt a kérésük, hogy „tanár elvtárs, olyan könyvet adjon a kezünkbe, amelyiket mi is megértünk”, mert ha úgy van benne, ahogy én elmondtam vagy a táblára írtam, akkor értették. Ilyen könyv akkoriban nem volt, de meghirdettek egy pályázatot, amelyre én elküldtem egy 24 oldalas anyagot, és engem választottak ki. Ez a kis könyvecske gyakorlatilag így készült el. Minden egyes része annak megfelelően lett megfogalmazva, magyarról magyarra fordítva, hogy a hallgatók megértsék, amit a klasszikus megfogalmazásból általában nem értettek meg.

Általános iskolától a középiskoláig – ha átnézem a könyveket – még sokszor találok olyan szöveget bennük, ami nem olyan egyszerű, nem lehet megérteni közvetlenül. Tehát a matematika tanítása során fontos, hogy legyenek olyan jól használható könyvek, nem a színessége vagy a képanyaga legyen vonzó, hanem a matematika szépsége legyen benne egy-egy példában. Ha ilyen módon az érdeklődést felkelti, akkor örömmel elolvassa a szöveget a diák is, és meglátja a jó rajzok alapján a változók közötti összefüggésket. Külön tehetség kell ahhoz is, hogy olyan rajzot tudjunk létrehozni, amelyik segíti a matematikának a megértését. Egy rajz (ábra) általában nemcsak változókat mutatja meg, hanem az a lényege, hogy milyen kapcsolat van a változók között. Ha ezt jól szemléltetem, akkor nagyon sokat segítettem a megoldáshoz. Köszönöm szépen a figyelmet!