Workshopok, bemutatók

2025 - Ollé Hajnalka – Spektroszkóp készítése. Interaktív workshop általános és középiskolás tanárok részére

Bevezetés

A jelenségek közti kapcsolatok felismerése elengedhetetlen ahhoz, hogy a diákok átfogó, napjaink kutatási eredményeihez hű képet alkothassanak a világról. Ezt csak oly módon lehet elérni, hogy egy konkrét természeti jelenséget részletesen tárgyalva eljutunk egy megállapításra, majd párhuzamot keresünk a fizika más területeivel, így a diákok maguk fedezhetik fel a törvényszerűséget, a kapcsolatot a fizika különböző fejezetei között. Ezt később általánosítva beépíthetik saját világképükbe. Ezúttal a spektroszkópia területét jártuk körül diákjaimmal.

A foglalkozások célja az volt, hogy az utat mutassam meg diákjaimnak, miként juthatnak el irányított, ám önálló munkával olyan felismerésekig, amelyek nemcsak pillanatnyi tanulmányaikat befolyásolják, hanem formálja a világszemléletüket, illetve fejleszti a problémamegoldó képességüket. Mindemellett fontos, hogy a munka befejeztével a diákok azt érezzék, ők is részesei lehettek egy tudományos igényű kutatómunkának, és alkottak valami hasznosat.

Ahogy a cím is sugallja, szerettük volna körül járni a spektroszkópia területét egészen a kezdetektől – tehát egy saját spektrum előállításától – a kitűzött cél eléréséig, miszerint a diákok által előállított spektrumot tudományos igényességgel feldolgozzuk és elemezzük. A diákok körében egyre népszerűbb a Python programozási nyelv, illetve az igény az alkotásra. Mindezeket felismerve és figyelembe véve született az ötlet, hogy készítsünk egy spektroszkópot, amit bárki otthon is megtehet, majd a kapott spektrum fotóját kiértékeljük különböző képfeldolgozási, illetve saját ötleten alapuló eljárások segítségével.

Elméleti háttér

Mielőtt a konkrét megvalósítást részleteznénk, az elméleti háttér tisztázása ugyanolyan fontos úgy a leírásban, mint a diákok számára is. A spektroszkópia témaköre sajnos nagyon elhanyagolt területe a fizikaoktatásnak. A standard fizikaórán csak érintőlegesen, vagy egyáltalán nem tanítjuk. Sokkal nagyobb hangsúlyt kellene fektetni a tárgyalására, hiszen rengeteg interdiszciplináris területen megjelenik, és felhasználhatósága gyakorlatilag határtalan. Ez köszönhető annak is, hogy az elmúlt kétszáz évben hatalmas fejlődésen ment keresztül.

A spektroszkópia a fény komponenseire való bontásával foglalkozik, így az atomoknak és molekuláknak a szerkezetéről, felépítéséről ad információt. Minden atomnak az egyedi struktúrájára jellemző színkép jelenik meg az elektromágneses spektrum skáláján. Ezt hasonlíthatnánk az emberek ujjlenyomatához, hiszen a spektrumvonal mintázat alapján beazonosítható a vizsgált atom vagy molekula.

A Bohr-féle atommodellben az atommag körül az elektronok csak bizonyos „megengedett” energiaszintű pályákon keringhetnek, hiszen az elektronok impulzusmomentuma (perdülete) kvantált, vagyis csak bizonyos diszkrét értékeket vehet fel, egészen konkrétan a Planck-állandó egész számú többszöröseit [1]. Egyszerűen fogalmazva, az atomon belül minden pályának megvan a rá jellemző energiaszintje, ahol az elektron stabilan tud keringeni. Ahogy haladunk az atommagtól kifelé, úgy nő a pályák energiaszintje.

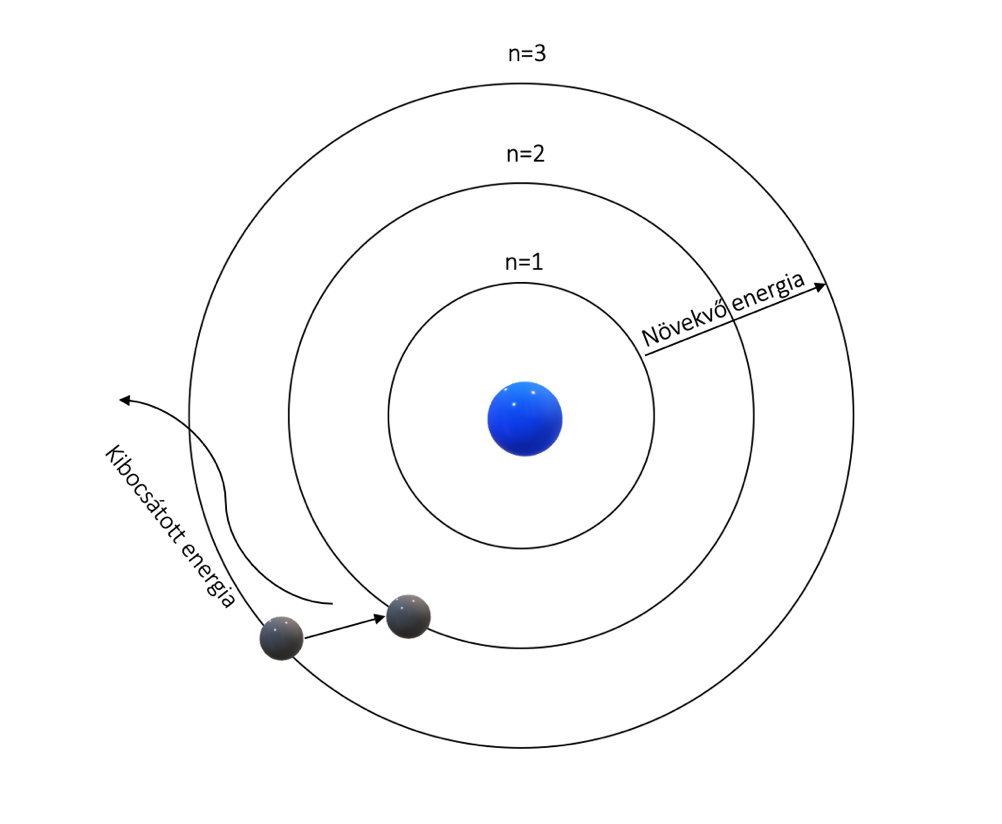
1. ábra: Az elektronpályák energia szerinti elrendeződésének modellje. Középen az atommag látható (kék), míg egy elektron alacsonyabb energiaszintű pályára ugrik, és az energiakülönbségnek megfelelő frekvenciájú elektromágneses sugárzást bocsát ki.

Energiafüggő intenzitásváltozást úgy érhetünk el, ha gerjesztett állapotba kerülnek az atomok, vagyis az atomban az elektronok. Ha egy elem forrón izzik, vagy egyéb módon energiát vesz fel, akkor az atommag körül keringő elektronok magasabb energiaszintű pályára ugranak. Ezt az állapotot nevezzük gerjesztett állapotnak. Viszont, - ahogy általánosan a természetre igaz – az elektronoknak nem kényelmes ez az állapot, hiszen energiaminimumra törekednek, így spontán visszaugranak az eredeti pályájukra, a fennmaradó felesleges energiát pedig foton, azaz fény formájában bocsátják ki (1. ábra). Ekkor az adott atomra jellemző frekvenciák fognak megjelenni a kibocsátott fény színképében. Ezt a színképet nevezzük emissziós spektrumnak. Azonban, ha egy forrón izzó gázon átvilágítunk, akkor a gáz a rá jellemző frekvenciákat elnyeli, így a fény, ami eljut hozzánk azokat a meghatározott frekvenciákat már nem fogja tartalmazni. A színképen fekete vonalak jelennek meg, ezt nevezzük abszorpciós spektrumnak [2] (2. ábra).

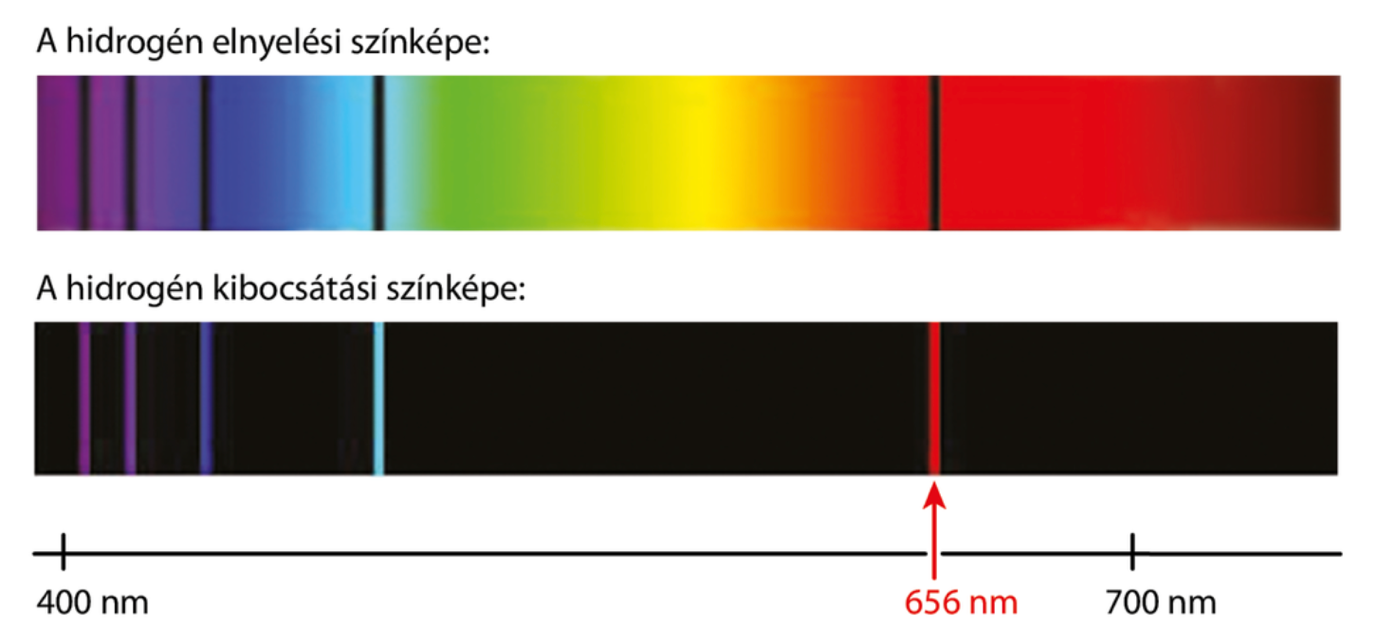
2.ábra: Felül a hidrogén elnyelési, alul pedig az kibocsátási színképe látható.

Az elemekre jellemző spektrumot jól ismerjük, így egy ismeretlen kémiai összetételű gáz spektrumának referenciaspektrumokkal való összehasonlítása célravezető lehet a beazonosítás szempontjából.

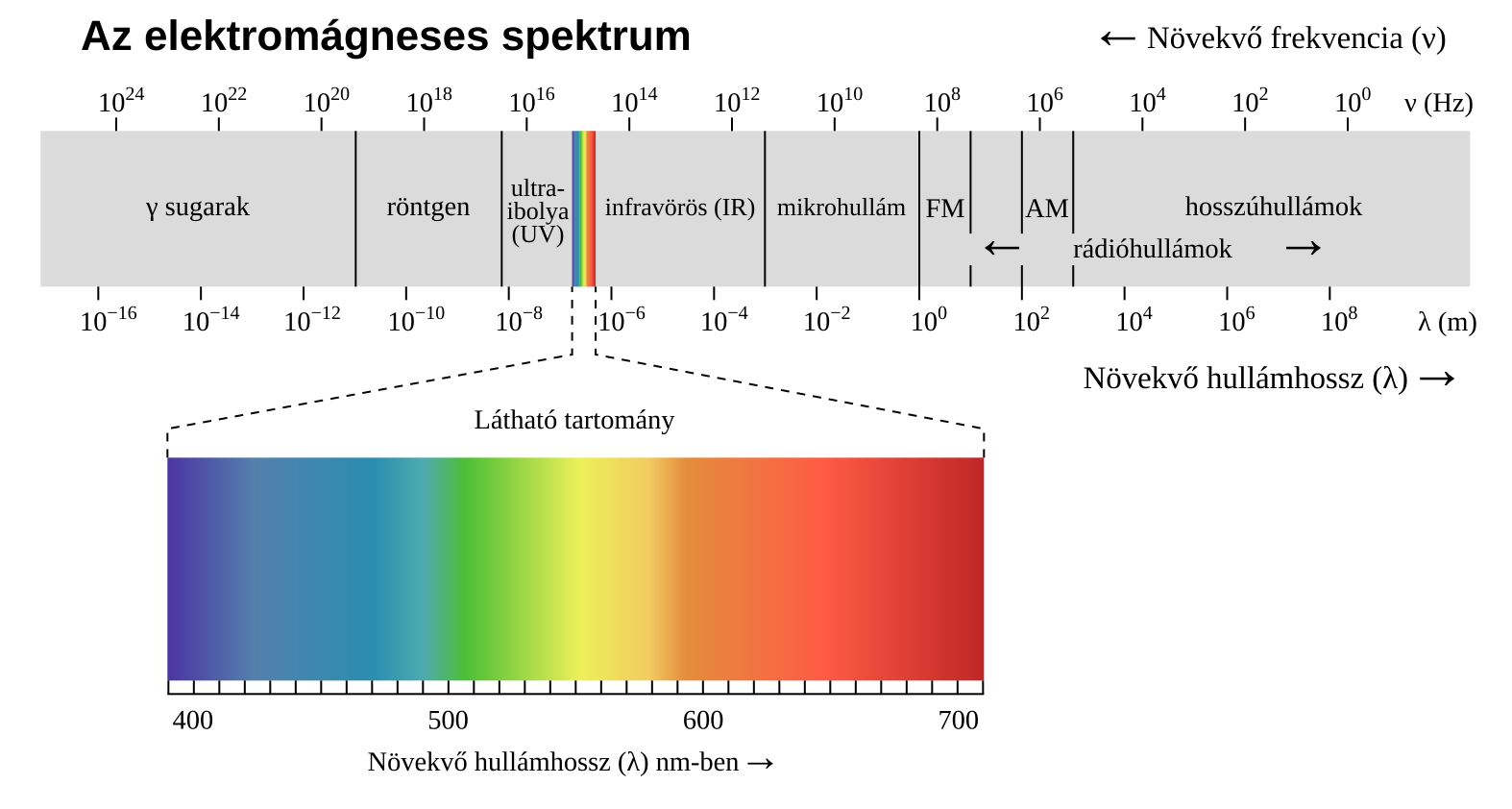
3. ábra: Az elektromágneses spektrum felosztása frekvencia szerinti tartományokra [3]

Az elektromágnesen spektrumon (3. ábra) a kibocsátott fotonok frekvenciája (vagy hullámhossza) látható. A hidrogénatom esetében, ha a gerjesztett elektron az első pályára ugrik vissza ultraibolya fény (Lymann-sorozat), ha a másodikra, látható fény (Balmer-sorozat), ha a harmadikra, akkor pedig infravörös fény (Paschen-sorozat) keletkezik [1,2].

Számunkra a látható tartományba eső spektrumvonalak lesznek érdekesek, hiszen a diákokkal megépített spektroszkóppal (melynek folyamatát a következő fejezet tárgyalja) készült fotókon csak azok jelennek meg. Mindemellett fontos tudatosítani, hogy spektrumvonalak megjelennek ultraibolya, illetve infravörös tartományban is.

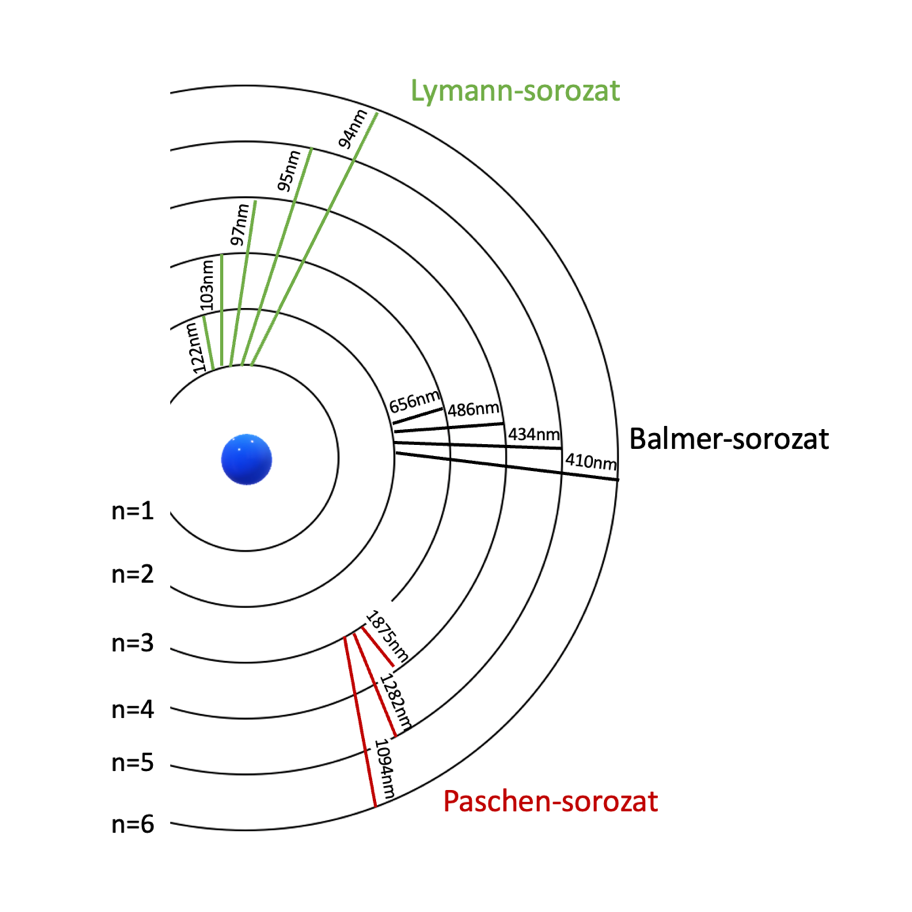
4. ábra: Ha az elektron a második pályára ugrik vissza, akkor az általa kibocsátott fény a látható tartományba esik.

Ezek az esetek alkotják a Balmer-sorozatot, mely fontos lesz a mi munkánk során is.

Az elektromágneses spektrumból nemcsak az atomokat tudjuk beazonosítani, a spektrum színképvonalai több információt is elárulnak. A hidrogén alfa vonala kiemelkedő figyelmet kap a csillagászati kutatások során. Ennek jelenlétét figyelik a csillagközi anyag térbeli eloszlásának feltérképezésénél. A hidrogén koncentrált jelenléte utalhat csillagkeletkezési régiók jelenlétére. Ebben helyi sűrűség-fluktuációkat figyelve a csillagkeletkezés korai szakasza figyelhető meg. Vonalak profilja különböző fizikai jelenségek hatására megváltozhat. Ha ezt összehasonlítjuk egy laboratóriumi körülmények között keletkező referencia vonalprofillal, akkor következtethetünk a vonal keletkezési helyének fizikai tulajdonságaira. Ezt kihasználva meghatározhatjuk például a csillagok forgási sebességét.

Ilyenkor a vonalprofil a Doppler-hatás miatt kiszélesedik, melynek mértékéből meghatározható a csillag forgási sebessége, továbbá az exobolygó keringési sebessége is. Ebben az esetben azt figyeljük, hogy a színképvonalak egyszerre tolódnak-e el a megszokott helyükről. Ha a hosszabb hullámhosszok felé, azaz a piros felé tolódnak, akkor a csillag távolodik tőlünk, tehát a bolygó közeledik. Ha rövidebb hullámhosszok felé tolódik, akkor értelem szerint fordítva [1]. Ennek az ide-oda mozgásnak lesz a bolygó keringési idejével megegyező periodicitása, tehát egyértelműen mutatja a keringési periódust. Ezen kívül a spektrumok elemzésével meghatározható például a csillagközi anyag kémiai összetétele is.

Spektroszkóp építése

Első lépésként egy saját spektrumot szerettünk volna előállítani. Az interneten rengeteg megoldás található olyan spektroszkópok építésére [4], melyek bárki számára elérhetőek, otthon fellelhető eszközökből könnyedén megépíthetők. Mi ezekből két változatot építettük meg. Mindkét spektroszkóp építésének részletes menetét bemutatjuk.

Spektroszkóp 1

Elkészítésénél nincs is másra szükség, mint egy CD lemezre, karton dobozra, optikai résre, vagy két darab egymással szembe fordított pengére, esetleg két műanyag kártyából is kialakítható a vékony rés, melyen a fény a dobozba kerül, ezen kívül henger alakú papír gurigára, szalagragasztóra, alufóliára.

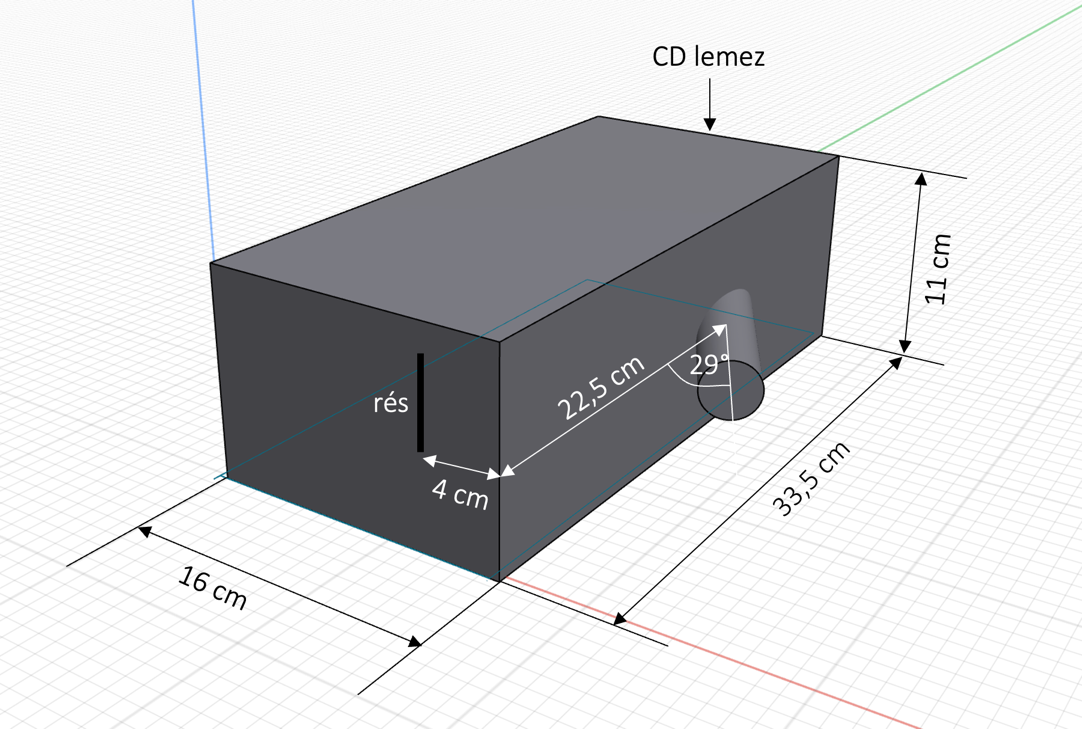
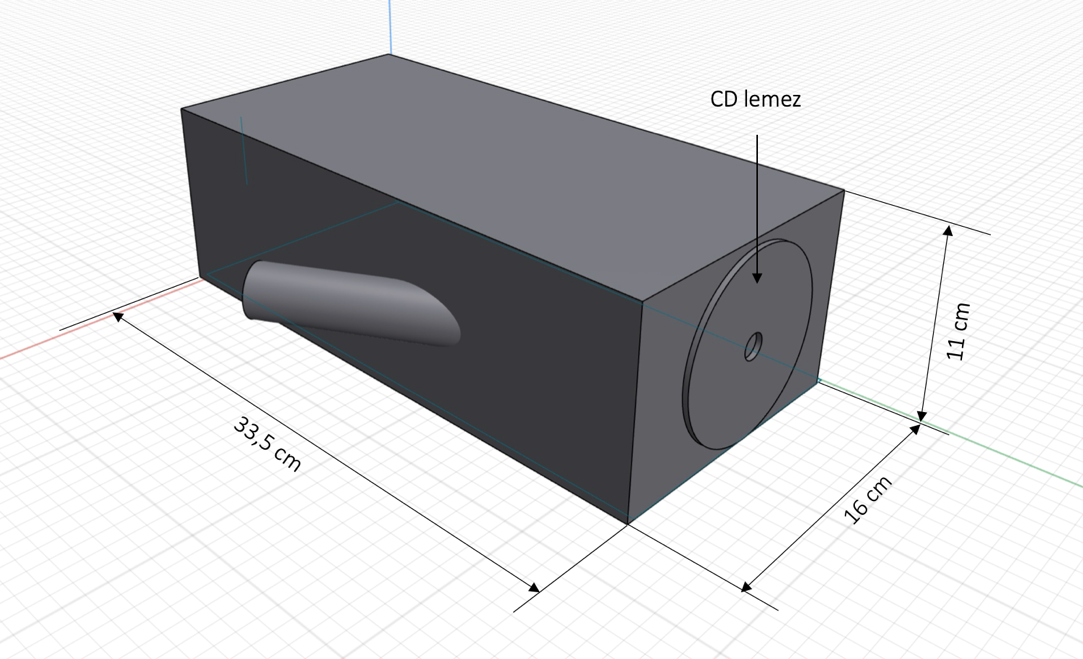
5. ábra: A téglatest alakúspektroszkóp sematikus ábrája

Az elkészítése nagyon egyszerű. Javaslom, hogy picit hosszabb karton dobozból készítsük. Az egyik végébe a CD lemezt erősítjük, a másik végén pedig a nyílást helyezzük el. Ennek sematikus vázlata az 5.ábrán látható.

A doboz egyik végébe, középre igazítva egy CD lemezt ragasztottunk. A vele szemközti oldalon, az ábrán látható módon aszimmetrikusan a doboz egyik széléhez közelebb kialakítunk egy rést, hogy a fénysugár a CD barázdáira essen, így az optikai rácsként viselkedve komponenseire bontja azt. Már csak a megfigyelő nyílás elhelyezése marad hátra. A mi esetünkben a papírgurigát 29°-ban elfordítva helyeztük a nyílásba. Szalagragasztóval rögzítettük. Itt egy picit próbálkozni kell, hiszem a doboz hosszától függ az, hogy mennyire széles tartományt látunk, illetve figyelembe kell venni a papírguriga anyagvastagságát is. A megépítés közben mi is vastagabbra cseréltük a látócsövet, mert a hidrogén jellegzetes kék és piros vonala nem látszódott egyszerre, csak részleteiben tudtuk megfigyelni a spektrumot.

Spektroszkóp 2:

Az első spektroszkóp tapasztalatait felhasználva ezúttal egy olyan eszközt szerettünk volna készíteni, ami egységesebb, és könnyebb használni. Éppen ezért olyan dobozt kerestünk, ami mindenki számára elérhető, és méretei egységesek, így nem kell sokat alakítani, testre szabni. Éppen ezért egy henger alakú chips-es dobozból alakítottuk ki a következő eljárással:

• A doboz egyik vége, konkrétan az alja, fém, így ebbe tudtunk egy vékony rést vágni szikével, ez szolgált optikai résként. Ezen a résen keresztül csak egy fénynyaláb jut át, ami pont a henger alakú doboz másik alapjára vetül.
• A doboz másik felébe CD-t illesztünk. A CD barázdái úgy működnek, mint egy optikai rács, ami fölbontja komponenseire a látható fényt, így ad ki egy spektrumot.
• A doboz oldalába egy másik hengert helyezük, amivel ráláthatunk a CD-re (amit a jobb fényképkészítés érdekében enyhén megdöntöttünk).
• Ügyelnünk kell arra, hogy a dobozba semmiféle más eredetű fénynyaláb ne kerülhessen, mert így kapunk zavartalan képet. Ez okból a dobozt kívülről fekete fóliával vonjuk be.

6. ábra: Segédeszközök, amikből a 2. spektroszkóp készült

 

7. ábra: Az összeállított spektroszkóp. Bal felén a CD, jobb felén a rés, és a hozzárendelt másik henger, melyen keresztül belátunk a spektroszkópba

Utolsó lépésként pedig fotókat készítettünk az iskola szertárában található kisülési csövek gerjesztett gázairól (8. ábra). A fotókat egyszerű mobiltelefonnal készítettük, mely a feldolgozásban semmilyen hátrányt nem jelentett. Az általunk írt python program kiválóan tudja alkalmazni a tömörített képformátumokat, pl. jpeg.

8. ábra: Gerjesztett neon gáz általunk előállított spektruma

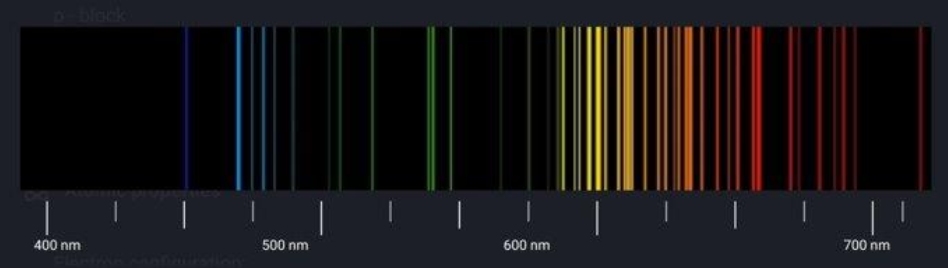
9. ábra: A neon referencia színképe [5,6]

10. ábra: Gerjesztett hidrogén gáz általunk előállított spektruma

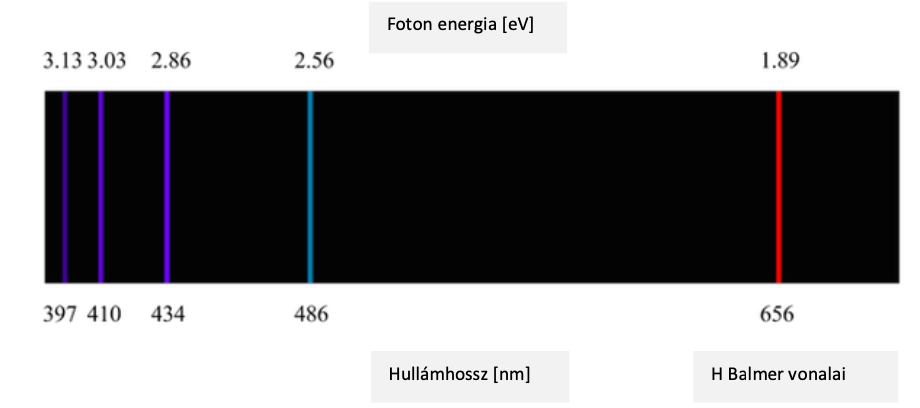
11. ábra: A hidrogén referenciaszínképe, jól összehasonlítható az általunk készített fotóval, ahol megjelennek a hidrogén α és β vonalai. [7]

Megfigyelés

Első lépésként a látható fényt figyeltük meg, ahol szépen látszott a folytonos spektrum. Végül – ami izgalmasabbnak bizonyult – a kisülési csöveket vizsgálatuk, amelyek minden középiskolai szertárban fellelhetők, így a kísérlet fizikaórán is egyszerűen bemutatható. A gázkisülési csövek különböző anyagi minőségű gázokat tartalmaztak, a mi esetünkben megfigyeltük a neon (8. ábra), a hidrogén (10. ábra), valamint a hélium, a higany, az argon és az oxigén emissziós vonalait (az utóbbiak fényképeit a cikk nem tartalmazza).

A diákok számára a neon volt a legérdekesebb, azt találták a legszebbnek, de fizikatanári szemmel be kell vallanom, a hidrogén volt a kedvencem. Gyönyörűen megjelentek a szemünk előtt a hidrogén látható tartományba eső Balmer-vonalai. Ezek a vonalak akkor keletkeznek, amikor a gerjesztett elektron a második pályára ugrik vissza, egy magasabb energiaszintű pályáról. Ha a hosszabb hullámhosszaktól a rövidebbek felé haladunk, akkor négy vonal látható a referenciaspektrumon: Hα (λ=656,3 nm), Hβ (λ=486,1 nm), Hγ (λ=434,0 nm), Hδ (λ=410,2 nm). Az általunk készített spektroszkópban a Hα, illetve Hβ egyértelműen világított. A másik két vonal intenzitása lényegesen gyengébb, így a spektroszkópunkban nem volt látható. Ennek az lehet az oka, hogy az osztályteremben, illetve a spektroszkóp dobozában nem volt tökéletesen sötét, így a beszűrődő természetes fényt egy gyenge kontinuumot adott a spektrumunknak (10. ábra bal felső része). Ebből a háttérből a Hγ és Hδ vonalak intenzitása nem tudott kiemelkedni, beleolvadt a háttérbe.

A hidrogén Balmer-sorozatának hullámhosszait a Rydberg-formula segítségével határozzuk meg [7]. Ez a Hα vonalra a következő:

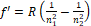
ahol f’ a spektrumvonal reciprokhullámhossza [7], azaz a frekvencia és a fénysebesség hányadosa, R a Rydberg-állandó, n₁ és n₂ pedig az elektronpályák sorszámai. Ha ezt a formulát alkalmazzuk a hidrogén alfa vonalára a következő értéket kapjuk:

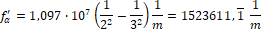
Melyből a hullámhossz:

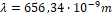
Ez a viszonylag egyszerű számolás jól érthetően bemutatja az egyes fogalmak jelentőségét, illetve a Rydberg-formula alkalmazásának mikéntjét.

Kapott fotók feldolgozása – Python-program létrehozása

Annak érdekében, hogy ezekből a spektrumokból információt tudjunk kinyerni, az elemzéshez szükségünk van egy számítógépes programra. A tervünk az, hogy a program úgy dolgozza fel az adott képet, hogy a spektrumból egy intenzitásgörbét rajzol fel, melyen megkeresi a csúcsokat. Az első megadott referenciakép beolvasásakor a program a csúcsok közti távolságokból arányokat készít, majd ezeket elmenti egy fájlba. Amikor egy általunk készített képet olvas be, majd az arányokat összehasonlítja a fájlban tárolt adatokkal, akkor annak a gáznak a nevét adja vissza, amelynek a referencia spektrumára legjobban hasonlít a spektrum, így képes megmondani, hogy a vizsgált spektrum milyen gáztól származik.

A képek feldolgozásához Python-nyelven írtunk programot, melynek működését a következő fejezetben részletesen tárgyaljuk. A képek készítésénél az az optimális, ha a vonalak pontosan függőlegesek és a háttér tökéletesen fekete. Ez nyilvánvalóan egy saját kép esetén majdnem lehetetlen, így csak bizonyos hibafaktorokon belül tudunk dolgozni.

• A program első lépésben beolvassa a képet, amit a szürke árnyalataiba konvertál, majd egy kicsit elhomályosítja, hogy ezzel szűrje a zajt és a kisebb hibákat a saját magunk által készített fotókról.
• Ezek után összegzi pixelenként az x-tengely mentén (a spektrum vonalaira merőlegesen) a pixelek értékét, amiből intenzitásgörbét rajzolhatunk fel. Ezen a görbén a program megkeresi a csúcsokat. Fontos, hogy a képből kivágunk egy szűk sávot, melyen az összes vonal szépen látható. Így a pixelek összegzése után az intenzitás ábrán szűkebbek lesznek a csúcsok (12. ábra alsó része).

A program működését először referencia spektrumokon teszteltük, majd később az általunk készített spektrumok képével is elvégeztük az elemzést, majd az összehasonlítást. Ezek eredményét a következő ábrák szemléltetik:

• A hélium spektruma

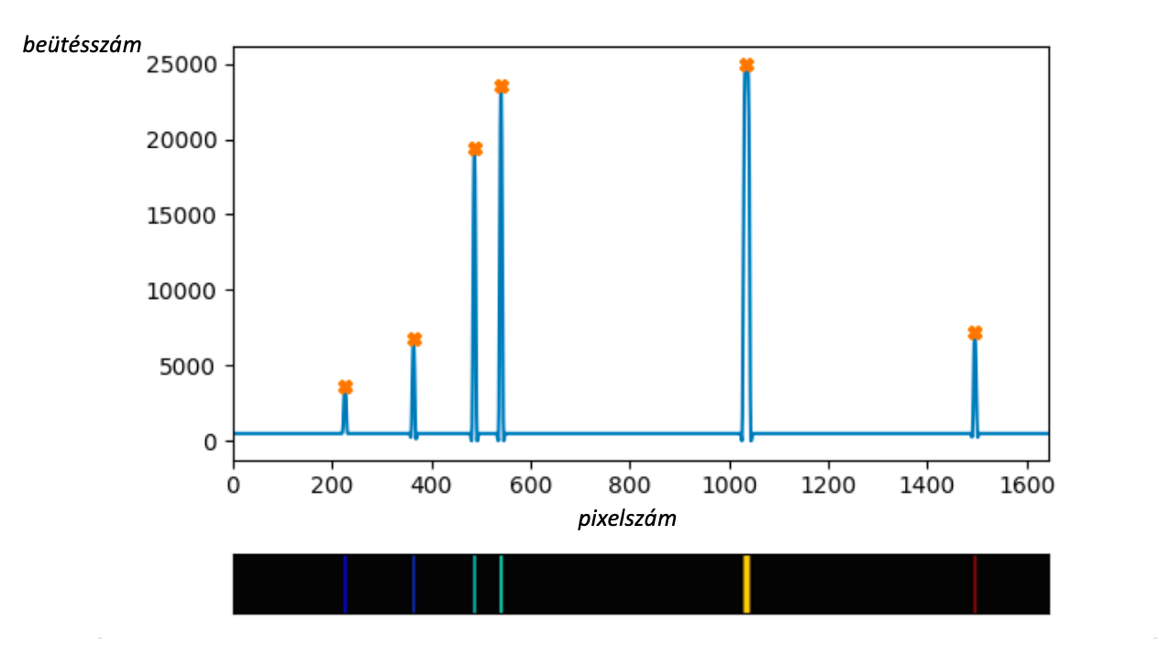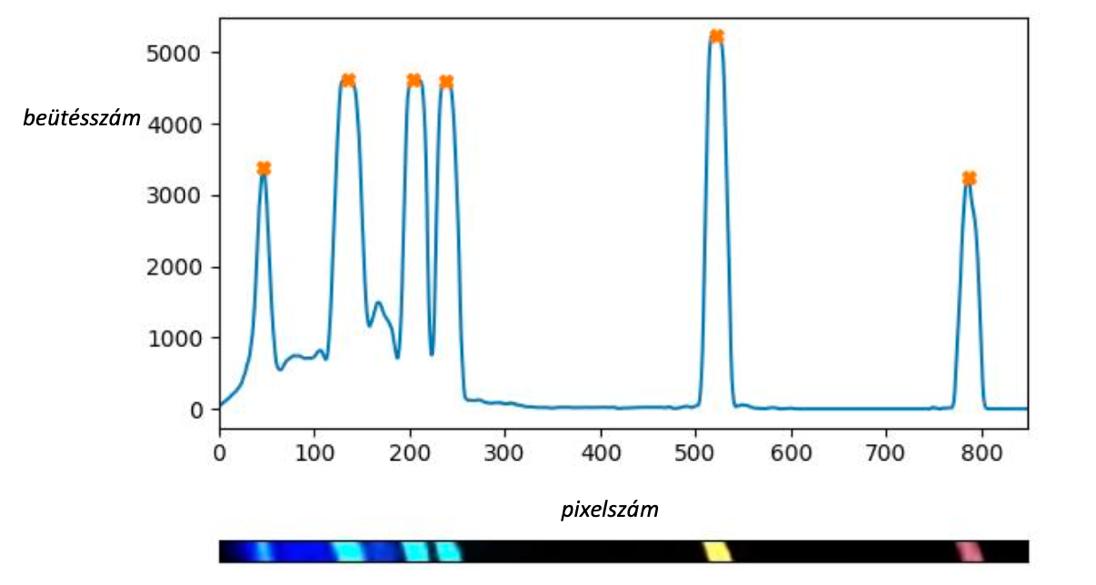6. ábra: Balra a hélium referencia spektruma [8], melynek vonalai az intenzitásgörbén tűként emelkednek ki. A jobb oldali ábrán pedig a hélium általunk készített spektrumának vonalai láthatók. A program itt is beazonosította a referenciaspektrumon is megtalált vonalakat. Az is megfigyelhető, hogy a saját spektrumunk bal széle (rövid hullámhosszoknál) az arányokat torzítja.

• A higany spektruma

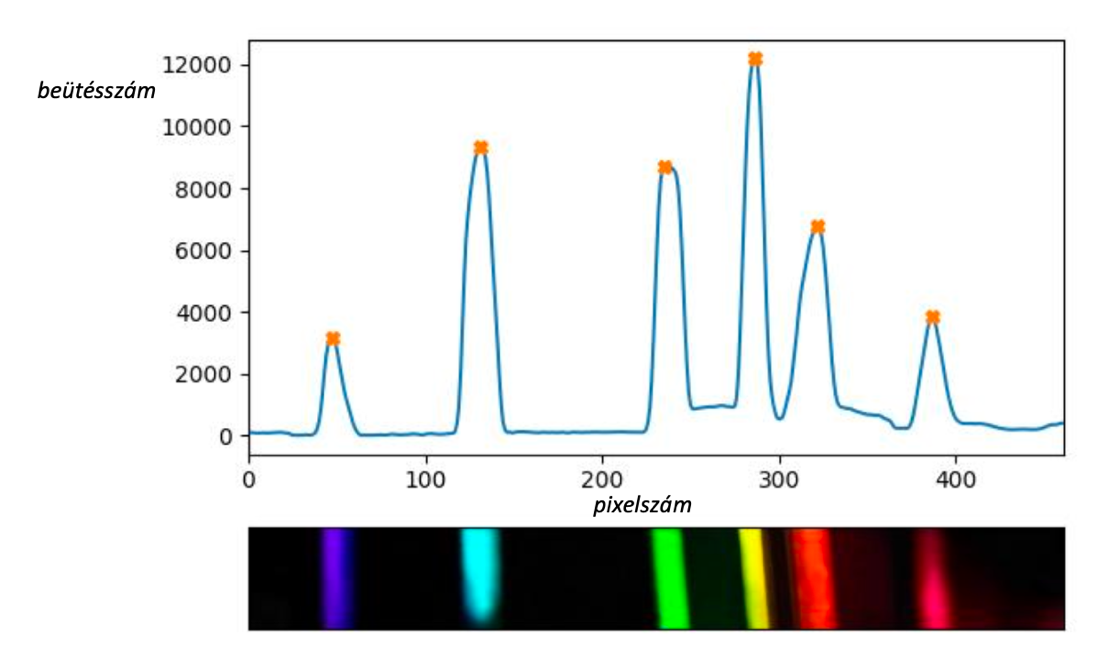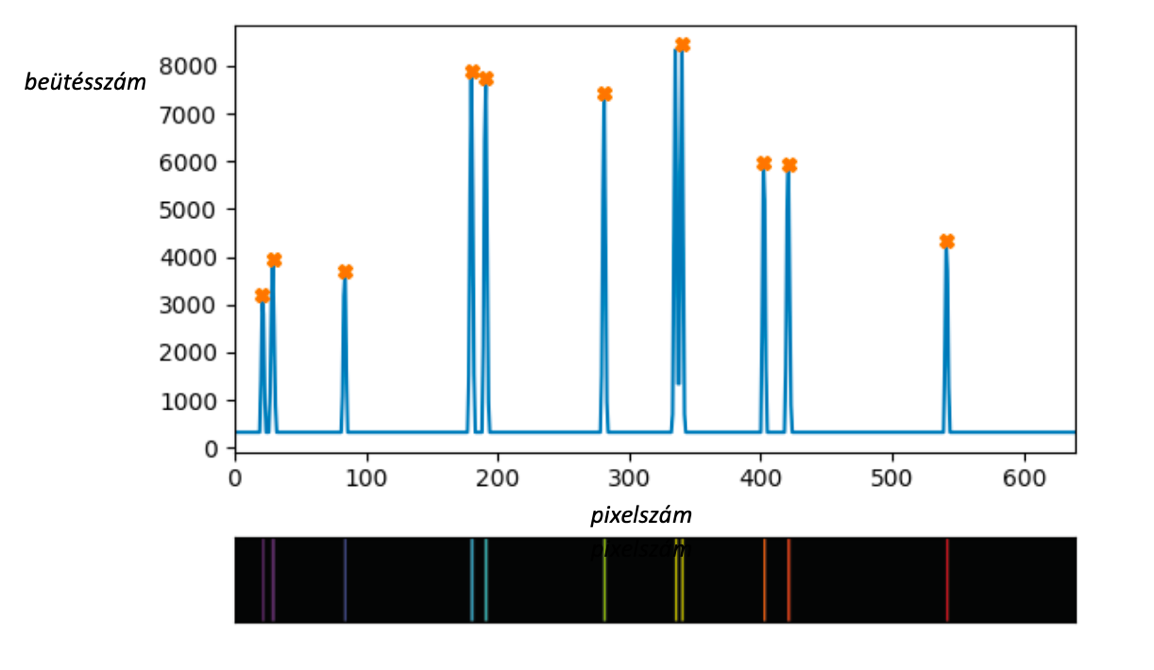
7. ábra: Balra a referenciaspektrum látható [9]. Ebben az esetben a higany színképét vizsgáltuk.

Jobbra pedig az általunk készített színkép.

Az alábbi táblázat bemutatja az általunk vizsgált spektrumokat, melyeket összehasonlítottunk a referencia spektrumokkal. Ezt úgy tettük meg, hogy a programmal meghatároztuk egy adott elem referencia spektrumán, illetve a saját spektrumunkon megtalálható vonalak helyzetét. Ez valójában úgy történik, hogy a meghatározott vonalcsúcshoz egy pixelszámot rendel. Mivel az általunk elkészített fotók és a referencia spektrum képe eltérő nagyságú, így az összehasonlításhoz két szomszédos vonal közti távolságot (pixelben) le kellett normálni az első és az utolsó vonal között pixeltávolsággal. Így egy arányszámot kapunk. Mivel a spektrumvonalak egymáshoz viszonyított helyzete arányaiban nézve állandó, így össze-hasonlíthatóvá vált a két spektrum. A táblázat magában foglalja ezeket, illetve az egyes elemek esetében az eltérés mértékét százalékban. A hidrogén esetében nagyon szép egyezést találtunk, de minél sűrűbb vonalrendszert találunk egy-egy spektrumon, annál nehezebbé válik a feladat. A fotók készítésénél különösen ügyelni kell a fekete háttérre, illetve a lehető legjobb felbontásra, hogy a készített spektrum és a referenciaspektrum közti eltérést a minimálisra csökkentjük.

Elem	Vonalak helye pixelekben						Eltérés
Hélium (referencia)	226	364	487	540	1033	1496	6%
Hélium (saját)	46	135	204	238	531	786
Higany (referencia)	98	326	543	667	840	1135	35%
Higany (saját)	63	191	355	428	480	580
Neon (referencia)	188	210	...*	415	425	478	48%
Neon (saját)	52	312	...**	814	866	1025

A táblázat összefoglalja a programunk által meghatározott elemek spektrumának eltérését százalékban, a referencia spektrumhoz képest. A Neon esetében helyszűke miatt a kimaradt értékek a következők:

*  233, 255, 267, 284, 301, 313, 330, 346, 373, 396

** 366, 421, 474, 508, 541, 587, 618, 659, 695, 762

A vonalak beazonosítása itt is viszonylag könnyen megy, de jelentkezik a meglehetősen nehéz rögzítés (fotózás) következménye, miszerint az egymáshoz nagyon közel álló vonalak már nem különülnek el. Ezeket már a program sem tudja bontani. Mindemellett a mi képünkön nem látható az első két vonal, valószínűleg azért, mert az nem az emberi szem által látható tartományokba esik, amikre a telefon kamerái is kalibrálva vannak.

További terv, hogy a program a spektrumra illesszen egy Planck-görbét. A Planck-görbe csúcsának helyéből (ahol a derivált nulla) megállapítható a gáz hőmérséklete. Ezáltal például egy csillag felszíni hőmérséklete.

Összefoglalás

Természetesen az általunk épített spektroszkóp nem alkalmas csillagászati mérésekre. Ennek technikai oka van, nem tudjuk egyetlen csillag fényét bevezetni a nyíláson, de az eljárások, kutatási módszerek bemutatására kiválóan alkalmas. Megismerteti a diákokat a kvantumfizika alapvető jelenségeivel, szemmel láthatóvá tesz olyan folyamatokat, melyekről eddig csak elméleti ismereteik voltak. Az oktatás során kiemelkedően fontos a szemléltetés, hiszen egy-egy jelenség, törvényszerűség így válik „kézzel foghatóvá”. Sokkal jobban rögzül a diákokban az ismeretanyag, ha képi megjelenítés vagy saját tapasztalat is társul hozzá.

A spektroszkópia tanítása rendkívül hasznos a fizikaoktatásban, mert nemcsak a fény és az anyag kölcsönhatásainak megértését segíti, hanem izgalmas, gyakorlati alkalmazásokkal is közelebb hozza a tudományt a diákokhoz. Összekapcsolja a természettudományokat, például a fizikát a kémiával (az atomszerkezet megismerésén és vizsgálatán keresztül), a csillagászattal (távoli égitestek összetételének elemzésével), a biológiával és az orvostudománnyal (például orvosi képalkotó eljárásokkal vagy biomolekulák vizsgálatával). A témakör szemléletes bemutatása segít a diákoknak megérteni, hogy a spektroszkópia nem csupán egy elméleti fogalom, hanem a mindennapokban is kulcsszerepet játszó tudományos, kutatási eszköz.

Felhasznált irodalom

• [1] D. Pavia, G. Lampman, G. Kriz, J. Vyvyan: Introduction to Spectroscopy, 5th edition, Cengage Leraning, 2014
• [2] Prabal Kumar Mallick: Fundamentals of Molecular Spectroscopy, Springer, Berlin 2023
• [3] https://commons.wikimedia.org/wiki/File:EM_spectrum_hu.svg
• [4] Pradip R. Gatkine, Gregorio Zimerman and Elizabeth Warner: A do-it-yourself spectrograph kit for educational outreach in optics and photonics, SPIE, September 2018.
• [5] https://wisc.pb.unizin.org/chem109fall2021ver02/chapter/atomic-spectra/
• [6] https://www.nagwa.com/en/explainers/469167813067/
• [7] https://franklyandjournal.wordpress.com/2016/07/18/hydrogen-spectrum/
• [8] http://astronomy.nmsu.edu/geas/lectures/lecture19/slide02.html
• [9] Jean Creighton: Survey of Astronomy, Chapter 5., 2019, Universities of Wisconsin https://wisconsin.pressbooks.pub/astronomy/chapter/chapter-5-5-3-spectroscopy-in-astronomy/

A program forráskódja (fejlesztés alatt)

import cv2

import numpy as np

import matplotlib.pyplot as plt

from scipy.signal import find_peaks

def ratio():

                    ratios = []

                    for i in peaks:

                                       ratios.append((int(i)/sum(peaks)) * 100)

                    print(ratios)

def add_to_database():

                    global ratios

                    file = open("source.txt", "a", encoding="UTF8")

                    name = input("Adja meg a referencia képen található gáz nevét: ")

                    print(name, end=" ", file=file)

                    for i in ratios:

                                       print(i, end=" ", file=file)

                    print()

img = cv2.imread('Photo/higany/higanynet1.png')

gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

blur = cv2.GaussianBlur(gray, (3,3), 0)

fig, (ax1, ax2) = plt.subplots(2, 1, gridspec_kw={'height_ratios': [3, 1]})

intensities = np.sum(blur, axis=0)

peaks, _ = find_peaks(intensities, prominence=img.shape[1],

distance=img.shape[1] / 100)

print(peaks)

ratio()

'''add_to_database()'''

ax1.plot(intensities)

ax1.plot(peaks, intensities[peaks], "X")

ax1.set_xlim([0, img.shape[1]])

ax2.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))

ax2.set_xticks([])

ax2.set_yticks([])

plt.show()